Welcome bla bla

I don't have much talent at web pages design, nor time, so don't expect too much. I just want to briefly describe the game and some technical aspects.
 

1. Game description

"Space Balls" is intended to be a 3D version of the game "Supaplex" or "Boulder Dash". Your main 'enemies' are the heavy balls you need to push around, and being a 3D game, they are in space. That's why "Space Balls". Your goal is to collect as many diamonds as necessary to complete the level.

Although it doesn't seem to be a difficult task, making such a game, I've encountered some very interesting problems, some of which I couldn't solve. But it's not a very difficult task either. This document is intended to give some technical hints to the not so experimented programmers. I would also like to hear from you, if you have some ideas that could help solve the open problems.
 

2. Genesis

The idea was given to me by Jake, one evening as we played some simple games on a palm top. And then I thought I could make a 3D version of Supaplex.
 

3. First steps

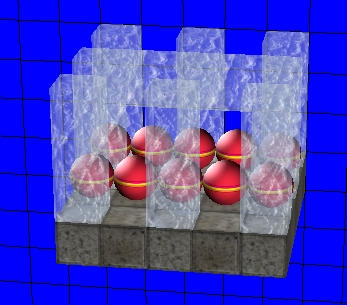
The transition from 2D to 3D is not easy. Because I wanted do make a very realistic game. First of all, comes the question: how do you see the scene in 3D ? Because in Supaplex you could see the whole screen, but in 3D there will always be hidden objects. Like in the pictures below, where you cannot easily guess what's behind the "base" cubes:
 
 

The answer came quickly: use some transparency. So the base cubes will be of two types: stone and ice for example. The pictures are not very accurate, due to the jpeg encoding, but you get the idea.
 

 The problem is the more transparent overlapping surfaces you render, the less you see through. That's why I had to remove the inner faces and vertices of every two adjacent cubes, so that I get as less faces as possible. This wasn't difficult at all, a trivial algorithm O(n2) worked just fine, provided the level dimensions are relatively small (max. 100). Plus, we send fewer vertices and faces to the renderer.
 

4. The speed problem

Even on my GeForce II GTS, rendering 1000 spheres (which is just a 10x10x10 cube), cca. 500 vertices each, could be a performance problem. And I wanted everything realistic, with textures, specular and lights. But the projection of a sphere is a circle, no matter from where you look, so the answer came easily: billboards.
For those who don't know, billboard is a technique used to improve performance on rendering particular objects, for example trees. It is actually a rectangular plane surface on which you apply a texture, and take care that it always faces you.
In this case, I rendered one sphere on an off screen surface, i.e. a bitmap. The background of this bitmap was green, and the size 128x128. Then, instead of spheres I render squares on the frame buffer, taking care that they always face the camera, i.e. not applying the rotation matrix. I apply the previously pre rendered texture on them doing a chroma keying on the green color.
Of course, there is a small deformation, due to the perspective projection. It goes more visible the further the spheres are from the center of the screen. But with a right projection angle and camera distance, it becomes unnoticeable.
Actually, provided we put some asymmetrical texture on the spheres, as in the pictures above, we need to pre render more then one sphere on off screen surfaces. This is because of the animation: the balls roll when they fall. But as we work in a discrete space, there will be relatively few different sphere positions, max. 25-30 I presume. 
 

5. The discrete space and the unsolved problems

If we take a look at Supaplex, we notice that the spheres can actually "stand" on top of each other, if they cannot fall anymore. Provided the low resolution of old VGA cards, and the fact that the spheres are not exactly circular in shape, it doesn't bother the eye. But in 3D it would look like this:

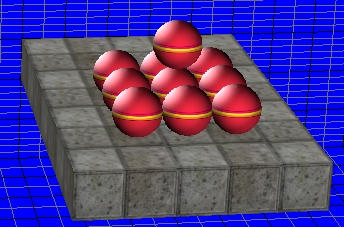
This is not realistic at all, and I wanted to make a realistic game. Which proved to be impossible.
Anyway, the stop positions should look like this:
 

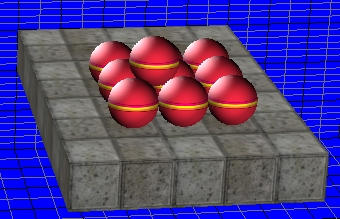That's more like it !
But, in the first example, the distance from the center of the top sphere to the floor is 1+sqrt(2), if we consider the radius of the sphere equals 1. In the second case, it's 1+sqrt(3). If they were on top of each other, it would be exactly 3.
As we know, sqrt(2) and sqrt(3) are irrational numbers, which means we cannot possibly align them on a grid, no matter how small the grid unit is. And we want to use a discrete space, we move our game character one unit at a time, either horizontally or vertically. Even if approximate sqrt(2)=1.42 and sqrt(3)=1.73 we cannot find a convenient grid unit.
The solution is to approximated a little more. I divided the base unit of the grid by 6 along the Y axis, and by 2 along X and Z. Now, I approximated sqrt(2)=1+4/6 and sqrt(3)=1+5/6 and I oversized the balls a little. This proved to be a good approximation, for the spheres appear to be tangent, as you can notice in the pictures. And the division on X and Z axis permits the intermediate positions in the first picture.
Plus, it opened a very large spectrum of possibilities of level design, some small horizontal or vertical bars like grates etc.
Until it proved to be not sufficient.
 

6. First animation problems

The size of the level I tested was 25x25x25. Using the division described above, I needed a matrix of 25x2x25x2x25x6 WORDS, which gives us about 732k of memory. As I made the animation, I was only concerned about the rendering speed, from the D3D point of view, and I ignored what the CPU and the rest of the system were doing, so I wrote:
for(i=0;i<dimx;i++)
    for(j=0;j<dimy;j++)
        for(k=0;k<dimy;k++)
            if(sphere_present_at_location_ijk) do_animation_stuff;

Big mistake, even from testing ! FPS was about 15-20, no matter how many spheres were moving.

I created immediately after that a linked list of moving objects and I got FPS of 180 ! About 10 times faster ! 
This demonstrates how important a data structure is, even for simple problems, let alone complex ones like BSP trees or octrees or whatever. And, by the way, I just wonder how can programmers using modern, pointer-less high level languages, very in vogue nowadays, can build this kind of structures. Are references really enough ? What about performance ?
 

7. Real animation problems and the impossibility to go on

Now comes the trouble: even in a discrete space the spheres can fall and land in a very large number of possibilities. And the grid setup above cannot handle all of them. Watch the following pictures:
 
 
 

Consider this position. The sphere on top can only fall towards us, and it will, for nothing is blocking it. After it falls, we get the position in the following picture.

Now watch the spheres closer to us. The distance between their centers is 1.5, considering the diameter of the balls (or the size of the grid) is 1.

Now, let's consider that a ball falls from above on top of the sphere to the left. It will hit this sphere and then it will fall aside. As the only free side is to the right, it will eventually land between the two spheres closer to us. It won't hit the ground, as the distance between them is 0.5 and not 1. So, it will remain suspended a little above the ground. This is of no concern for the time being, let's just evaluate the X coordinate of the sphere's center. As the distance is 1/2 and it falls exactly in the middle, this coordinate will be something+1/4. Hmm, but our grid smallest unit on X and Z is 0.5, so we cannot align this sphere to our grid. If we divide the grid in 4, we can find similar examples where the center of a certain sphere needs to be something+1/8. And so on, and so on. This is the point where I got stuck. I demonstrated actually that it's not possible to have tangent spheres in a discrete space, even with a good approximation.

7+1 is missing

(read Terry Pratchett for an explanation)
 

9. Conclusion

There are two ways out of this dead end. First one is to give up the discrete space. There will be no grid, objects can have any shape and position and so on. With a good collision detection algorithm, it's not a big problem to make it. But I want to make a mere game and not a falling balls simulator ! I don't know how playable the thing will be. Plus the level design will be a pain in the ass, as well as solving the puzzle itself.

The second way is to stick to the "ball on top of other ball doesn't fall" assumption, and with some tricks to render them as naturally as possible. I choose this way, because I don't like letting things unfinished.

I decided to port the so far coded game to OpenGL, so that NT users and UNIX users can play it. And in my opinion D3D 7 is far from the performance, accuracy and easiness of OpenGL. That's why I won't continue, nor publish the D3D version. 

If someone has bright ideas or wants the D3D sources, just mail me.